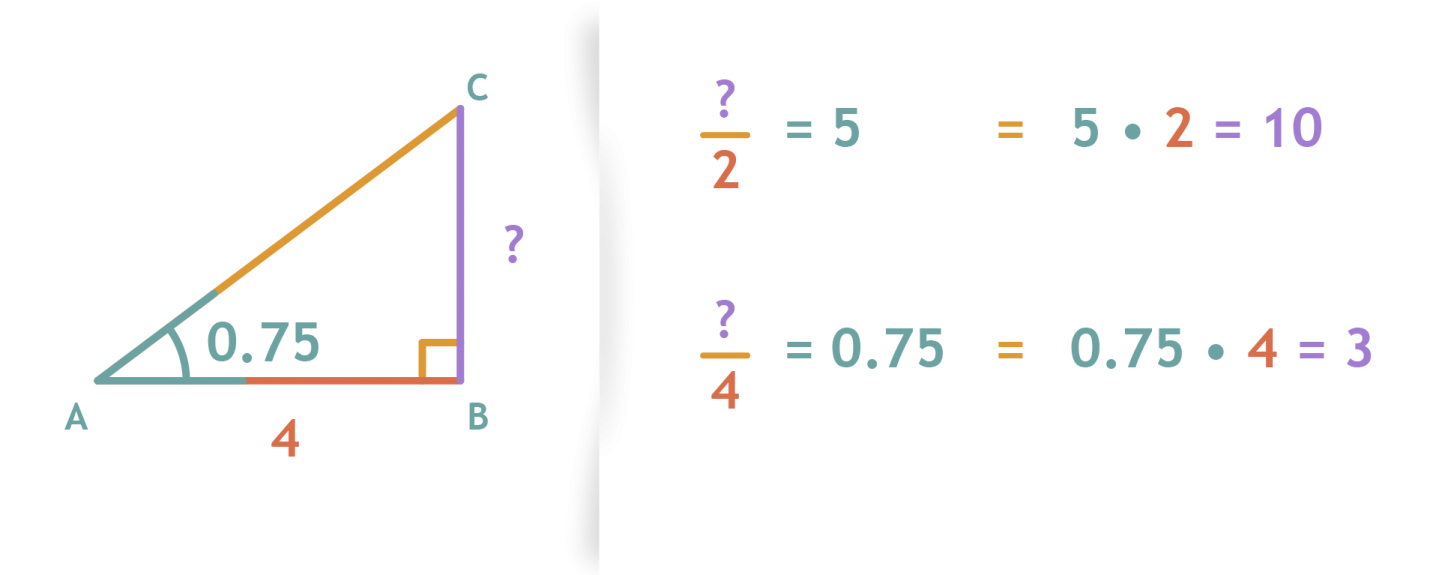Hoe Cos Maken Met Tan En Sin
We weten dat tansin cos.
Hoe cos maken met tan en sin. Bijvoorbeeld de sinus van 30. Met tan sin en cos kun je veel problemen oplossen In dit voorbeeld weet je dat de hoek 63 graden en de aanliggende rechthoekzijde 5 centimeter is. Toegevoegd na 1 minuut.
Met de t-formules zo genoemd vanwege de substitutie. Gebruik een eenvoudige SIN-functie met een gemakkelijk te onthouden antwoord. En zoals je misschien al hebt geraden zijn deze drie verhoudingen niets anders dan de sinus cosinus en tangens.
Bfmboxsin angleA frac. Toegepast op onze driehoek. Cos-1 arccos acos Sin-1 arcsin asin.
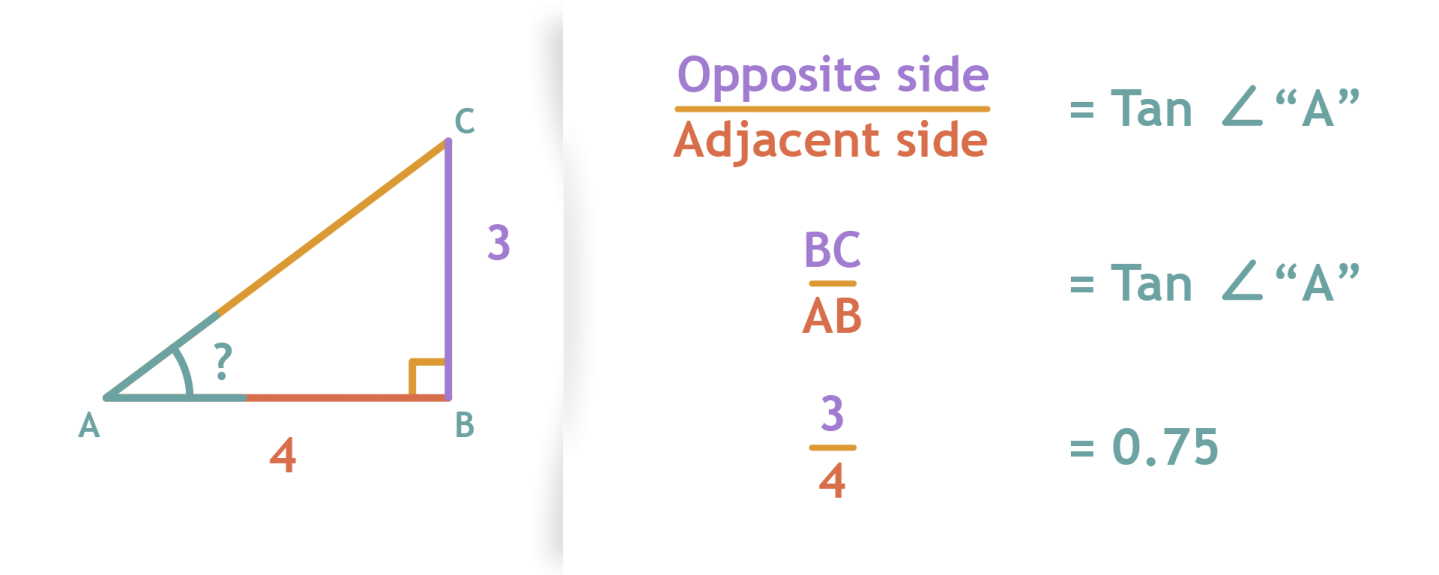
Hiervoor waren de volgende formules van belang. Dit toegepast op de volgende driehoek voor hoek α krijg je volgend resultaat. Wanneer je van een rechthoekige driehoek de lengtes van de zijdes weet kan je de hoek berekenen door middel van de inverse van de sinus cosinus of tangens sin 1 cos 1 tan 1.
Zie het onderstaande rekenvoorbeeld. Cos cos 2 sin cos 3 sin sin 2 sin cos 2 2 2 xx xx x x x x S S SS S S S S. Tom gi Overige TSO-BSO - maandag 9 juni 2003 Antwoord Beste Tom Je hebt verschillende driehoeken.
B Geef die waarden in je figuur aan. Bepaal of je hiervoor eerst 30 moet intoetsen of eerst op SIN moet drukken. In de formule om dit te berekenen hoeven we dus alleen gebruik te maken van de schuine zijde en de aanliggende rechthoekzijde.
Elk type verhouding heeft een naam gekregen. Bij het gebruiken van de SIN COS en TAN-functies zal je twee verschillende dingen moeten onthouden. Als je een hoek en een zijde weet dan kan je de andere zijdes uitrekenen met sinus cosinus of tangens.
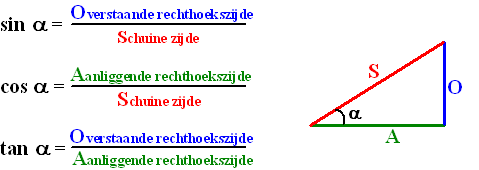
We korten sinus af met sin cosinus met cos en tangens met tan. In deze theorie leggen we je uit hoe de lengte van de zijden van een rechthoekige driehoek kunt berekenen met behulp van de sinus cosinus en tangens. τρεῖς treis drie γωνία gōnia hoek en μετρεῖν metrein meten of driehoeksmeetkunde is een tak van de wiskunde die zich bezighoudt met driehoeken en in het bijzonder de oorspronkelijk op driehoeken gebaseerde goniometrische functies zoals sinus sin cosinus cos en tangens tan.
Maar we willen graag de lengte van de schuine zijde berekenen. Dus voor elke hoek neem je de sinus en deel je deze door de waarde van cosinus voor de overeenkomstige waarde van tangens. Cos 3012 3213.
Methode De sinus cosinus en tangens geven allen de verhouding aan tussen. 1 sin 1 sin 22 cos cot sec 1 sec 1 DD DD DD 3. In deze theorie leggen we je de basis uit van hoe je met de sinus cosinus en tangens kunt werken om zo elke scherpe hoek van een rechthoekige driehoek te kunnen berekenen.
Dit is een basisvak van de vlakke meetkunde. A Laat je rekenmachine sin110 en cos110 bepalen in twee decimalen. Je doet cos-1 door op je rekenmachine eerst shift en dan cos in te toeten Zijde berekenen.
Dus de cosinus van A is 069. De volgorde van de knoppen en radialen versus graden. A is dan cos-1 069 46.
Tan-1 is de omgekeerde bewerking van Tan. We hebben geleerd hoe je hoeken kunt berekenen met behulp van de sinus cosinus en tangens. Sinus cosinus en tangens.
Met sinus cosinus en tangens werken. Tan 45 1 tan-1 1 45. T tan 1 2 x displaystyle ttantfrac 12x zijn vergelijkingen met goniometrische identiteiten in x displaystyle x op te lossen door ze eerst te schrijven als functie van t displaystyle t en later weer terug te transformeren naar x displaystyle x.
Toegevoegd na 2 minuten. Sinus cosinus en tangens Hoe zie ik wanneer ik cos sin of tan moet gebruiken bij een driehoek. C Leg uit dat voor hoeken tussen 90.
Vanzelfsprekend geven we bij iedere video een aantal voorbeeldopgaven waarbij we deze nieuwe kennis direct toepassen. Teken een cirkel met straal 1 en een lijnstuk OP met lengte 1 en een richtingshoek van 110. In sommige situaties kun je ook te maken krijgen met goniometrische vergelijkingen van de vorm sinA sinB of cosA cosB.
Hoe je dit soort vergelijkingen op kunt lossen zie je in uitlegvideo 8. Ongelijkzijdige driehoeken gelijkbenige driehoeken gelijkzijdige driehoeken scherpe driehoeken rechthoekige driehoeken en stompe driehoeken. In de eerste extra opgaven kun je zien hoe bijvoorbeeld Ptolemaeus en Hipparchos de sinus gebruikten om afstanden en afmetingen van hemellichamen te bepalen.
Je kunt dit ook andersom gebruiken. Deze kan je op je rekenmachine vinden door eerst de shift in te drukken en vervolgens sin cos of tan. Sec tan 1 sin sec tan 2 sec tan 1 sin D D D DD D D D 4.
De cosinus van de hoek negatief en de sinus van de hoek positief is. Voor Cos en Sin geldt hetzelfde. 2 D1 tan 3 1 cot sec 2tan tan D D D D 273 Vereenvoudig volgende uitdrukkingen steunend op de formules voor aanverwante hoeken.
Bijvoorbeeld tan 30sin 30.